Sliced Optimal Transport Sampling

Loïs Paulin¹ Nicolas Bonneel¹ David Coeurjolly¹ Jean-Claude Iehl¹ Antoine Webanck¹ Mathieu Desbrun² Victor Ostromoukhov¹

¹Université de Lyon, CNRS, LIRIS, France ²ShanghaiTech/Caltech

In ACM Transactions on Graphics (Proceedings of SIGGRAPH), 2020

Sliced Optimal Transport Sampling. Global illumination of a scene (top left, San Miguel) requires integrating radiance over a high-dimensional space of light paths. The projective variant of our sliced optimal transport (SOT) sampling technique, leveraging the particular nature of integral evaluation in rendering and further combined with a micro-Cranley-Patterson rotation per pixel, outperforms standard Monte Carlo and Quasi-Monte Carlo techniques, exhibiting less noise and no structured artifact (top right, 32spp) while offering a better spatial distribution of error (bottom right, errors from blue (small) to red (large)). Moreover, our projective SOT sampling produces better convergence of the mean absolute error for the central 7×7 zone of the highlighted reference window as a function of the number of samples per pixel (from 4spp to 4096spp, bottom-left graph) in the case of indirect lighting with one bounce.

Abstract

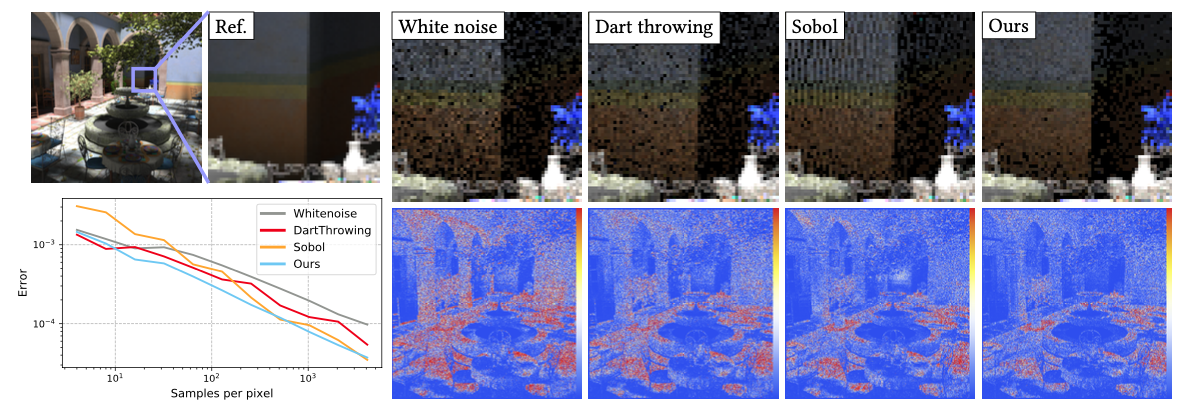
In this paper, we introduce a numerical technique to generate sample distributions in arbitrary dimension for improved accuracy of Monte Carlo integration. We point out that optimal transport offers theoretical bounds on Monte Carlo integration error, and that the recently-introduced numerical framework of sliced optimal transport (SOT) allows us to formulate a novel and efficient approach to generating well-distributed high-dimensional pointsets. The resulting sliced optimal transport sampling, solely involving repeated 1D solves, is particularly simple and efficient for the common case of a uniform density over a d-dimensional ball. We also construct a volume- preserving map from a d-ball to a d-cube (generalizing the Shirley-Chiu mapping to arbitrary dimensions) to offer fast SOT sampling over d-cubes. We provide ample numerical evidence of the improvement in Monte Carlo integration accuracy that SOT sampling brings compared to existing QMC techniques, and derive a projective variant for rendering which rivals, and at times outperforms, current sampling strategies using low-discrepancy sequences or optimized samples.

Downloads

Publication:
Code:
- Sampler Source Code

Reference

Loïs Paulin, Nicolas Bonneel, David Coeurjolly, Jean-Claude Iehl, Antoine Webanck, Mathieu Desbrun, Victor Ostromoukhov. Sliced Optimal Transport Sampling. ACM Transactions on Graphics (Proceedings of SIGGRAPH), 39(4), July 2020.

@article{paulin2020,
    author = "Paulin, Loïs and Bonneel, Nicolas and Coeurjolly, David and Iehl, Jean-Claude and Webanck, Antoine and Desbrun, Mathieu and Ostromoukhov, Victor",
    title = "Sliced Optimal Transport Sampling",
    journal = "{ACM} Transactions on Graphics (Proceedings of SIGGRAPH)",
    year = "2020",
    volume = "39",
    number = "4",
    month = jul,
    abstract = "In this paper, we introduce a numerical technique to generate sample distributions in arbitrary dimension for improved accuracy of Monte Carlo integration. We point out that optimal transport offers theoretical bounds on Monte Carlo integration error, and that the recently-introduced numerical framework of sliced optimal transport (SOT) allows us to formulate a novel and efficient approach to generating well-distributed high-dimensional pointsets. The resulting sliced optimal transport sampling, solely involving repeated 1D solves, is particularly simple and efficient for the common case of a uniform density over a d-dimensional ball. We also construct a volume- preserving map from a d-ball to a d-cube (generalizing the Shirley-Chiu mapping to arbitrary dimensions) to offer fast SOT sampling over d-cubes. We provide ample numerical evidence of the improvement in Monte Carlo integration accuracy that SOT sampling brings compared to existing QMC techniques, and derive a projective variant for rendering which rivals, and at times outperforms, current sampling strategies using low-discrepancy sequences or optimized samples."
}

Citation(s)

Google scholar citations: ...